Implementing a small physics engine for a platformer game
Note: The full content of this post is available on https://marc-fr.github.io/Website_MarcGames/devlog_impulse.html (the link is subject to change)
The aim is to simulate the motion of a vessel, that evolves in a uniform gravity field and in a static world.
1. Integration of the motion
The state of a rigid body is defined by the position of its center of inertia and its rotation. With only the gravity, the motion can be integrated with the exact integration scheme:
void simulate_1(float dt)
{
// Motion integration
bodyPos += dt * bodyVel;
bodyRot += dt * bodyRotVel;
// Gravity
bodyPos += 0.5 * dt * dt * gravity;
bodyVel += gravity * dt;
// [...]
}
2. Computing a contact response
When the body hits a fixed obstacle, a reaction force prevents penetration. With the rigid body approximation, the velocity of the body has a gap at the hit time. Consequently, the contact response is defined by a velocity gap. From the integration of the equation of motion, I use the approximation of a single force, with a constant direction. After some maths, I obtain the following code:
const float moverI = 0.20f;// (depends on the object geometry)
void simulate_2(float dt)
{
// [...] Motion integration + Gravity
// Contact
dvel = vec2(0.f, 0.f);
drotvel = 0.f;
for (cnt in compute_contacts())
{
// Rebound
const float reboundCoef = 1.2f; // (depends on the surface's type)
float alpha = cnt.normal.x * ( cnt.pt.y*cnt.pt.x*cnt.normal.y - cnt.pt.y*cnt.pt.y*cnt.normal.x) +
cnt.normal.y * (-cnt.pt.x*cnt.pt.x*cnt.normal.y + cnt.pt.x*cnt.pt.y*cnt.normal.x);
alpha = 1.f - moverI * alpha;
dvel.x -= dot(cnt.vit,cnt.normal) * reboundCoef / alpha * cnt.normal.x;
dvel.y -= dot(cnt.vit,cnt.normal) * reboundCoef / alpha * cnt.normal.y;
const float fmoment = cnt.pt.x * cnt.normal.y - cnt.pt.y * cnt.normal.x;
drotvel -= moverI * dot(cnt.vit,cnt.normal) * reboundCoef / alpha * fmoment;
// Friction
const float frictionCoef = 0.1f; // (depends on the surface's type)
float alphaT = cnt.tangent.x * ( cnt.pt.y*cnt.pt.x*cnt.tangent.y - cnt.pt.y*cnt.pt.y*cnt.tangent.x) +
cnt.tangent.y * (-cnt.pt.x*cnt.pt.x*cnt.tangent.y + cnt.pt.x*cnt.pt.y*cnt.tangent.x);
alphaT = 1.f - moverI * alphaT;
dvel.x -= dot(cnt.vit,cnt.tangent) * frictionCoef / alphaT * cnt.tangent.x;
dvel.y -= dot(cnt.vit,cnt.tangent) * frictionCoef / alphaT * cnt.tangent.y;
const float fmomentT = (cnt.pt.x * cnt.tangent.y - cnt.pt.y * cnt.tangent.x);
drotvel -= moverI * dot(cnt.vit,cnt.tangent) * frictionCoef / alphaT * fmomentT;
}
bodyVel += dvel;
bodyRotVel += drotvel;
}
Results and discussion:
While a single simulatenaous contact is made, this method will yield good results. However, it can produce overreaction with multiple simultaneous contacts, since the body's velocity is not updated between each contact evaluation.
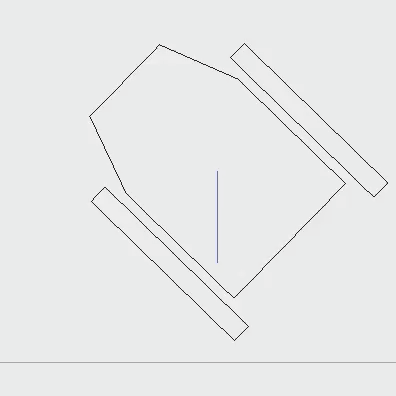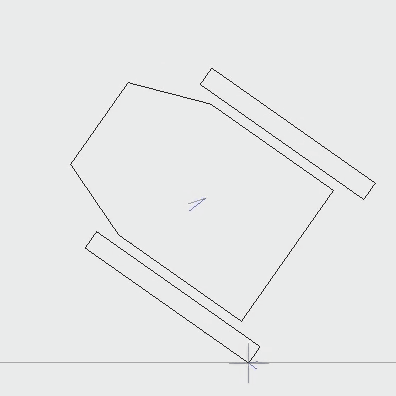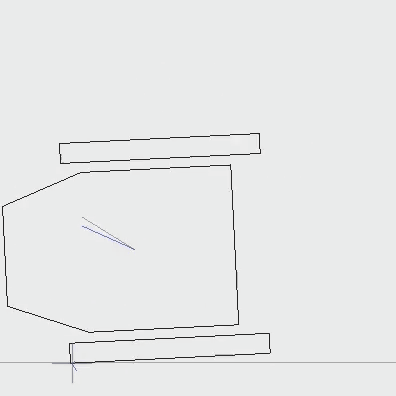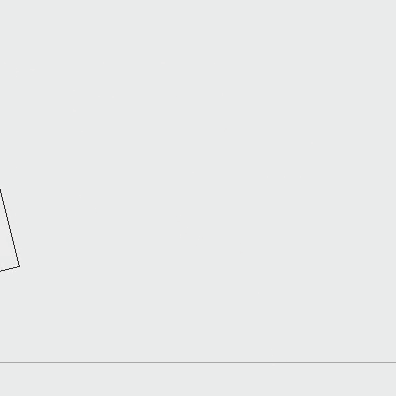
3. Resolution of the penetration
There are 2 methods to compute the penetration. The first method is to compute the exact time when the body enters in contact and to split the time-frame simulation in two parts, before and after the contact. The second method is to work with the penetration at the end of the timeframe, so after a little while of the hit time.
I decided to go with the second method,
because it allows to easily work with multiple contacts and its good stability when the body stands on the ground.
However, the penetration resolution may fail to be resolved if the time-step or the velocity is too high.
As such one or two steps of the first method can be applied to have a state that is closer to the hit, and therefore obtain more precision.
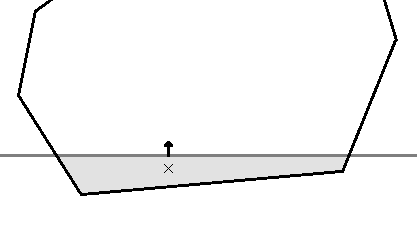
Unfortunately, the contact location is not a single point but a surface, thus a virtual contact-point must be determined. (The contact force is applied from it.) This point is calculated by the barycenter of the intersecting area.
After this, the body must be moved to cancel the penetration. I choose the simplest way: translate the body along the obstacle normal vector, such that it no longer penetrates the obstacle.
void simulate_3(float dt)
{
// [...] Motion integration + Gravity
// Contact
dpos = vec2(0.f, 0.f);
for (cnt in compute_contacts())
{
// [...] Rebound
// [...] Friction
// Compute variation of displacement - only translation
dpos.x += cnt.penet * cnt.normal.x;
dpos.y += cnt.penet * cnt.normal.y;
}
bodyPos += dpos;
}
Concerning the contact algorithm, the code is available in TRE.
Results and discussion:
Like with the velocity computation, the displacement method will produce over-displacement when there are multiple contacts.
But because the displacements are likely not noticeable, it will still produce good results.
However, the rotational velocity and velocity-gap are ignored.
Then the scheme tends to produce an unwanted forward motion when the body has contact-points that last several timeframes.
I may work in the future to improve the scheme, by properly taking the rotational velocity into account.
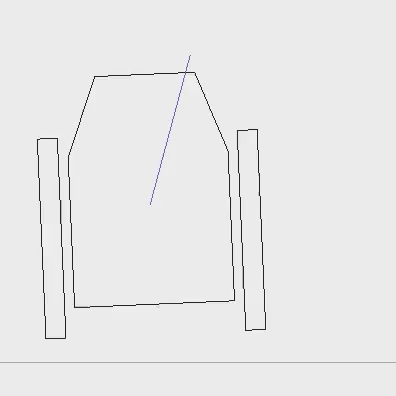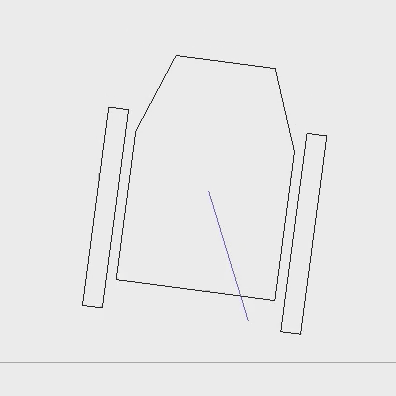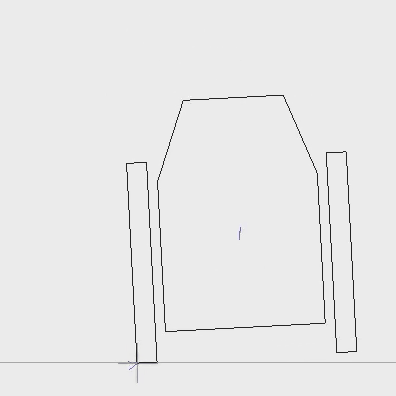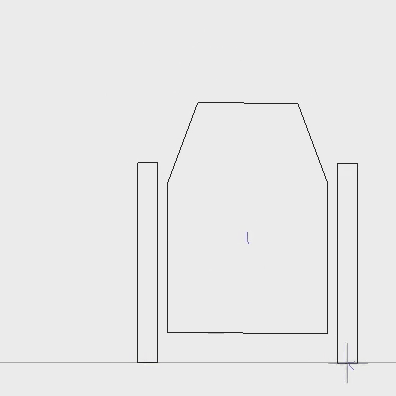
4. Faking the landing feet
Adding landing feet with dampers greatly improves the feeling of the contact response. The coupling between the vessel and the feet is not obvious to determine. However, I use a conjectured method to keep it simple and compatible with the kinetic relations established above.
The principle is to use what I call a "transmittance" factor between the foot and the body. When the foot's spring is no stressed, the contact force is completely received by the foot, and the vessel does not perceive the contact force. Conversely, the contact force is fully transmitted to the vessel when the foot reaches its maximal displacement. The coupling is made by forcing the vertical position of the foot.
void simulate_4(float dt)
{
// [...] Motion integration + Gravity
// Foot motion (left/right)
foot.pos += dt * foot.vel;
foot.vel += dt * ( -16.f * foot.pos - 3.1f * m_foot.vel);
foot.pos = clamp(foot.pos, -1, 1);
// Contact
for (cnt in compute_contacts())
{
const float dvproj = dot(cnt.vit,vesselup);
const float dyproj = dot(cnt.normal,vesselup);
if (is_foot)
{
float footpart = 1.f; // Transmission factor
footpart = 1.f - max(foot.pos, 0.f) * 1.f;// (foot amplitude is [-1,1] around equilibrum)
footpart = 1.f - (1.f - footpart) * (1.f - footpart); // arbitrary law
footNew.pos += footpart * dyproj * cnt.penet;
footNew.vel -= footpart * dvproj * (reboundCoef - 1.f); // this helps for stability
// remaining part is passed to the vessel
cnt.penet -= footpart * dyproj * cnt.penet;
cnt.vit -= footpart * dvproj * vesselup;
}
// [...] Rebound
// [...] Friction
// [...] Displacement
}
footNew = foot;
}
Results and discussion:
Despite this simple and naive approach, the results are good enough.
Get MoonLanding Project
MoonLanding Project
platformer with the lunar landing module
| Status | Released |
| Author | lanocram |
| Genre | Platformer |
| Tags | emscripten, Gravity, hard, moon, Physics, Singleplayer, Space, webgl |
| Languages | English, French |
| Accessibility | Interactive tutorial |
More posts
- Main Release 2.080 days ago
- Main Release 1.0Dec 30, 2023

Leave a comment
Log in with itch.io to leave a comment.